时间复杂度 n^2表示n的平方,选择排序有时叫做直接选择排序或简单选择排序
| 排序方法 | 平均时间 | 最好时间 | 最坏时间 | 空间复杂度 |
|---|---|---|---|---|
| 桶排序(不稳定) | O(n) | O(n) | O(n) | O(1) |
| 基数排序(稳定) | O(n) | O(n) | O(n) | O(n) |
| 归并排序(稳定) | O(nlogn) | O(nlogn) | O(nlogn) | O(n) |
| 快速排序(不稳定) | O(nlogn) | O(nlogn) | O(n^2) | O(logn) |
| 堆排序(不稳定) | O(nlogn) | O(nlogn) | O(nlogn) | O(1) |
| 希尔排序(不稳定) | O(n^1.25) | O(1) | ||
| 冒泡排序(稳定) | O(n^2) | O(n) | O(n^2) | O(1) |
| 选择排序(不稳定) | O(n^2) | O(n^2) | O(n^2) | O(1) |
| 直接插入排序(稳定) | O(n^2) | O(n) | O(n^2) | O(1) |
\omicron
O(n)这样的标志叫做渐近时间复杂度,是个近似值.各种渐近时间复杂度由小到大的顺序如下
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
一般时间复杂度到了2^n(指数阶)及更大的时间复杂度,这样的算法我们基本上不会用了,太不实用了.比如递归实现的汉诺塔问题算法就是O(2^n).
平方阶(n^2)的算法是勉强能用,而nlogn及更小的时间复杂度算法那就是非常高效的算法了啊
冒泡排序,简单选择排序,堆排序,直接插入排序,希尔排序的空间复杂度为O(1),因为需要一个临时变量来交换元素位置,(另外遍历序列时自然少不了用一个变量来做索引)
快速排序空间复杂度为logn(因为递归调用了) ,归并排序空间复杂是O(n),需要一个大小为n的临时数组.
基数排序的空间复杂是O(n),桶排序的空间复杂度不确定
所有排序算法中最快的应该是桶排序(很多人误以为是快速排序,实际上不是.不过实际应用中快速排序用的多)但桶排序一般用的不多,因为有几个比较大的缺陷.
1.待排序的元素不能是负数,小数.
2.空间复杂度不确定,要看待排序元素中最大值是多少.
所需要的辅助数组大小即为最大元素的值.
SkipList 跳表
在计算机科学领域,跳跃链表是一种数据结构,允许快速查询一个有序连续元素的数据链表。快速查询是通过维护一个多层次的链表,且每一层链表中的元素是前一层链表元素的子集。
基于并联的链表,其效率可比拟于二叉查找树(对于大多数操作需要O(logn)平均时间)。
基本上,跳跃列表是对有序的链表增加上附加的前进链接,增加是以随机化的方式进行的,所以在列表中的查找可以快速的跳过部分列表,因此得名。所有操作都以对数随机化的时间进行。
下面的结构是就是跳表:
其中 -1 表示 INT_MIN, 链表的最小值,1 表示 INT_MAX,链表的最大值。
(1) 由很多层结构组成
(2) 每一层都是一个有序的链表
(3) 最底层(Level 1)的链表包含所有元素
(4) 如果一个元素出现在 Level i 的链表中,则它在 Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
例子:查找元素 117
(1) 比较 21, 比 21 大,往后面找
(2) 比较 37, 比 37大,比链表最大值小,从 37 的下面一层开始找
(3) 比较 71, 比 71 大,比链表最大值小,从 71 的下面一层开始找
(4) 比较 85, 比 85 大,从后面找
(5) 比较 117, 等于 117, 找到了节点。
http://kenby.iteye.com/blog/1187303
java 并发包 Skip list(跳表)是一种可以代替平衡树的数据结构,默认是按照Key值升序的。Skip list让已排序的数据分布在多层链表中,以0-1随机数决定一个数据的向上攀升与否,通过“空间来换取时间”的一个算法,在每个节点中增加了向前的指针,在插入、删除、查找时可以忽略一些不可能涉及到的结点,从而提高了效率。
在Java的API中已经有了实现:分别是
ConcurrentSkipListMap(在功能上对应HashTable、HashMap、TreeMap) ;
ConcurrentSkipListSet(在功能上对应HashSet).
确切来说,SkipList更像Java中的TreeMap,TreeMap基于红黑树(一种自平衡二叉查找树)实现的,时间复杂度平均能达到O(log n)。
HashMap是基于散列表实现的,时间复杂度平均能达到O(1)。
ConcurrentSkipListMap是基于跳表实现的,时间复杂度平均能达到O(log n)。
ConcurrentSkipListMap和TreeMap类似,它们虽然都是有序的哈希表。
但是,第一,它们的线程安全机制不同,TreeMap是非线程安全的,而ConcurrentSkipListMap是线程安全的。
第二,ConcurrentSkipListMap是通过跳表实现的,而TreeMap是通过红黑树实现的。
//代码实现
最常用方法:定义两个指针,同时从链表的头节点出发, 一个指针一次走一步,另一个指针一次走两步。 如果走得快的指针追上了走得慢的指针,那么链表就是环形链表; 如果走得快的指针走到了链表的末尾(next指向 NULL)都没有追上第一个指针,那么链表就不是环形链表。
但是这里需要返回存在的环的开始节点(确认环的位置)。此时有两种情况
- 链表头尾相连,这个很简单最后得到的就是出现环的节点
- 链表的尾与链表中间的节点出现环
public boolean hasCircle (ListNode head) {
boolean isHasCircle = false;
// 链表为空
if (head == null) {
return false;
}
//指向链表的头部
ListNode p1 = head;
//指向链表的头部
ListNode p2 = head;
//不为空执行while循环
while (p2 != null) {
if (p2.next == null || p2.next.next == null) {
return false;
}
// p1 一次移动一步
p1 = p1.next;
// p2一次移动两步
p2 = p2.next.next;
//单链表有环
if (p1 == p2){
isHasCircle = true;
break;
}
}
if (isHasCircle) {
// 查找环的入口点,
p1 = head;
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
System.out.println(p1.data);
}
return isHasCircle;
}
class ListNode{
public int data;
public ListNode next;
public ListNode (int data){
this.data = data;
}
@Override
public String toString (){
return "->" + data;
}
}
https://www.zybuluo.com/867976167/note/52199
//代码实现
前序遍历:若二叉树为空,则空操作返回null。否则先访问根节点,然后前序遍历左子树,再前序遍历右子树
中序遍历:若二叉树为空,则空操作返回null。否则从根节点开始,中序遍历根节点左子树,然后访问根节点,最后中序遍历右子树
后序遍历:若二叉树为空,则空操作返回null。否则以从左到右先叶子后节点的方式遍历访问左右子树,最后访问根节点
层序遍历:若树为空,空操作返回null。否则从树的第一层,也就是根节点开始访问,从上而下逐层遍历,在同一层中,从左到右对结点逐个访问
-
前序
-
中序
-
后序
https://blog.csdn.net/jsqfengbao/article/details/47393151
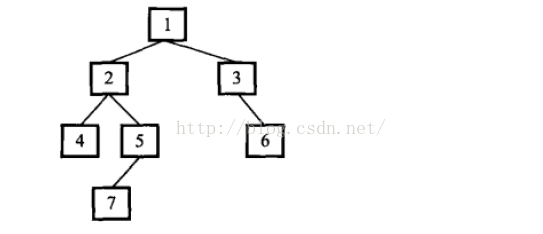
例如,如下图的二叉树的深度为4, 因为它从根节点到叶结点的最长的路径包含4个结点(从根结点1开始,经过2和结点5,最终到达叶结点7).
我们可以从另一种角度来理解树的深度。 如果一棵树只有一个结点,它的深度为1, 如果根节点只有左子树而没有右子树, 那么树的深度应该是其左子树的深度+1.同样如果根节点只有右子树而没有左子树,那么树的深度应该是其右子树+1.如果既有左子树又有右子树, 那概述的深度就是左、右子树的深度的较大值加1.。
利用这个思路,我们可以用递归来实现代码
//普通二叉树求深度
public int treeDepth(BinaryTreeNode root){
if(root == null)
return 0;
int nLeft = treeDepth(root.leftNode);
int nRight = treeDepth(root.rightNode);
return (nLeft > nRight)?(nLeft+1):(nRight+1);
}
我们用后序遍历的方式遍历二叉树的每个结点, 在遍历一个结点之前我们就已经遍历了它的左右子树。 只要在遍历每个结点的时候我们记录它的深度(某一节点的深度等于它到叶结点的路径的长度), 我们就可以一边遍历一边判断每个结点是不是平衡二叉树。下面是这种思路的实现代码:
//高效率的判断是否是一棵平衡二叉树
public boolean isBalanced2(BinaryTreeNode root){
int depth = 0;
return isBalanced2(root,depth);
}
public boolean isBalanced2(BinaryTreeNode root,int depth){
if(root == null){
depth = 0;
return true;
}
int left = 0,right = 0;
if(isBalanced2(root.leftNode,left) && isBalanced2(root.rightNode,right)){
int diff = left-right;
if(diff <= 1 && diff >= -1){
depth = 1+(left > right?left : right);
return true;
}
}
return false;
}
在上面的代码中,我们用后序遍历的方式遍历整棵二叉树。 在遍历某结点的左右子树结点之后, 我们就可以根据它的左右子树的深度判断它时不时平衡的, 并得到当前结点的深度。 当最后遍历到树的根节点的时候,也就判断了整棵二叉树是不是平衡二叉树。
https://blog.csdn.net/crazy1235/article/details/66971177
1、最简单的方式,想到的方式,通过stack来入栈出栈操作实现。
2、循环迭代方式。
3、递归方式
递归方式有两种, 一种是从前向后,另一种是从后向前。
扩展
https://leetcode.com/problems/reverse-linked-list/
https://leetcode.com/problems/reverse-linked-list-ii/description/
Reverse a linked list from position m to n. Do it in-place and in one-pass.
For example:
Given 1->2->3->4->5->NULL, m = 2 and n = 4,
return 1->4->3->2->5->NULL.
Note:
Given m, n satisfy the following condition:
1 ≤ m ≤ n ≤ length of list.
反转链表中第m 到 第n 个结点
解决方案就是通过链表反转的方式,将m-n个结点反转,然后在拼接之前后之后的结点。
重点就是记录第m个结点的前驱结点和第n个结点的后续结点。