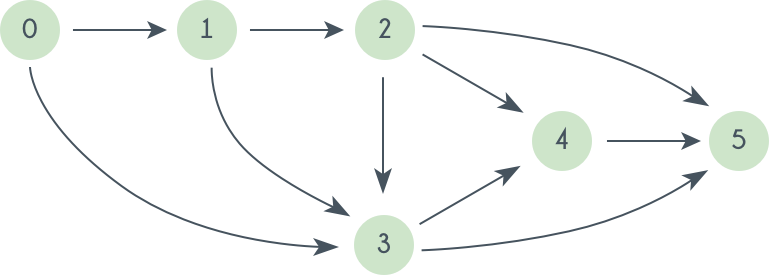
Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge uv, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.
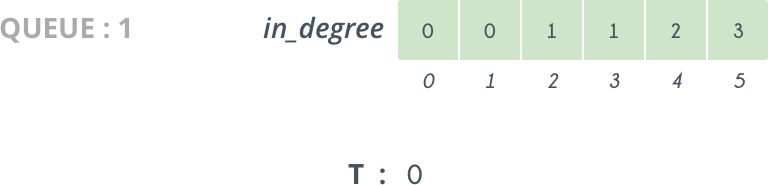
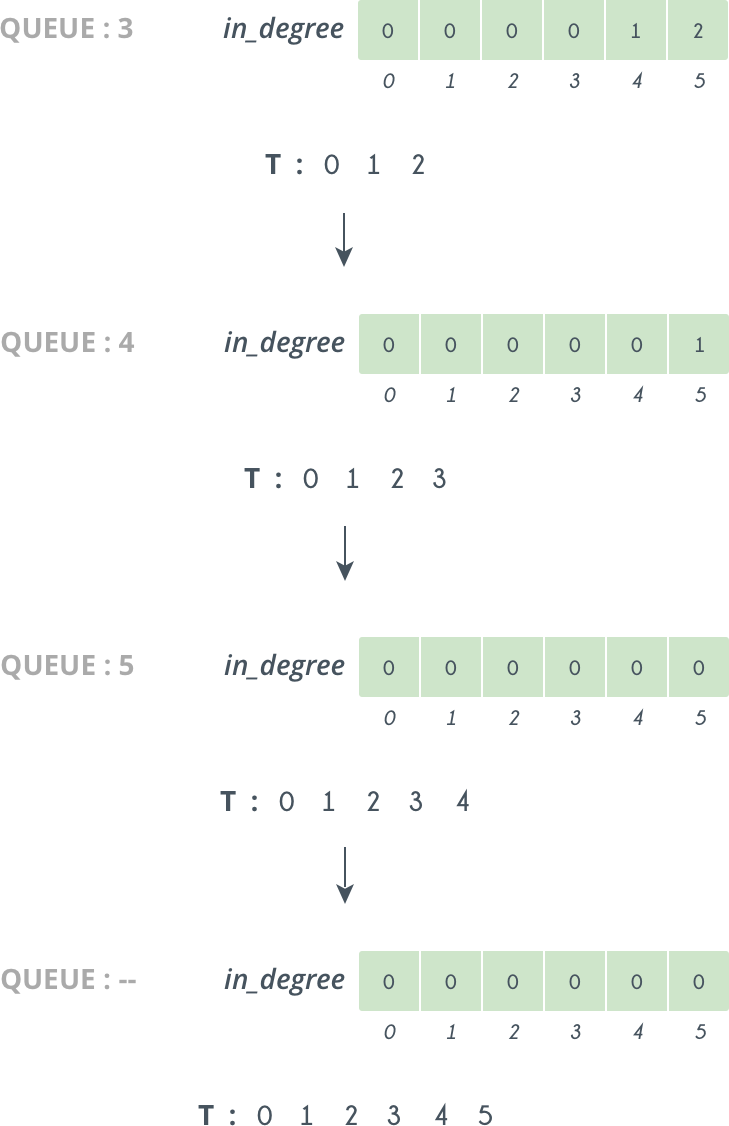
- Find any vertex v with in-degree zero
- Add v in sorted array
- Remove vertex v and all edges emanating from it from the directed graph
- Repeat from Step 1, until all vertices have been added to sorted array
Total Time = O(|V|^2 + |E|) Here, O(|V|^2) is the time complexity for finding a vertex with in-degree zero, and O(|E|) is the time complexity for reducing in-degree of all the adjacent vertices by one on deletion of the vertex.