Read More
想了解光线追踪，你可以环顾四周，找到被光线照亮的物体，沿着到达视点的光线反方向进行追踪，就是光线追踪。
光线追踪和光栅化， 是两种不同的成像方式。
光线追踪能解决全局效果的场景 (尤其是间接光照很合适, 当然并不是说光栅化就不能做全局光照)
一般认为光栅化是属于快速近似. 并不是那么精细. 而光线追踪追求更加真实. 光栅化对于全局的情况处理的不好， 比如半影，全局光照等。
glossy 表示有点反光, 但是又有些粗糙的物体 (铜镜)
早期人类认为人能看见物体, 是因为眼睛发出光线, 看到物体之后再返回来. 这和现在的常识不符.
PS：所以光线追踪的思想是感知光线
光线追踪是跟踪眼睛发出的光线( 这点似乎和常识有点不同, 是由于光路可逆 ) 到达物体的过程
PS: 在这里的光线追踪基于下面三个假设
- 光线直线传播（尽管物理上并不是）
- 光线不会发生碰撞 （或者说光线相交了但是互不影响 尽管物理上不是）
- 光线从光源传播到人的眼睛
光线的一个性质: 光路可逆 (也就是追踪的意思)
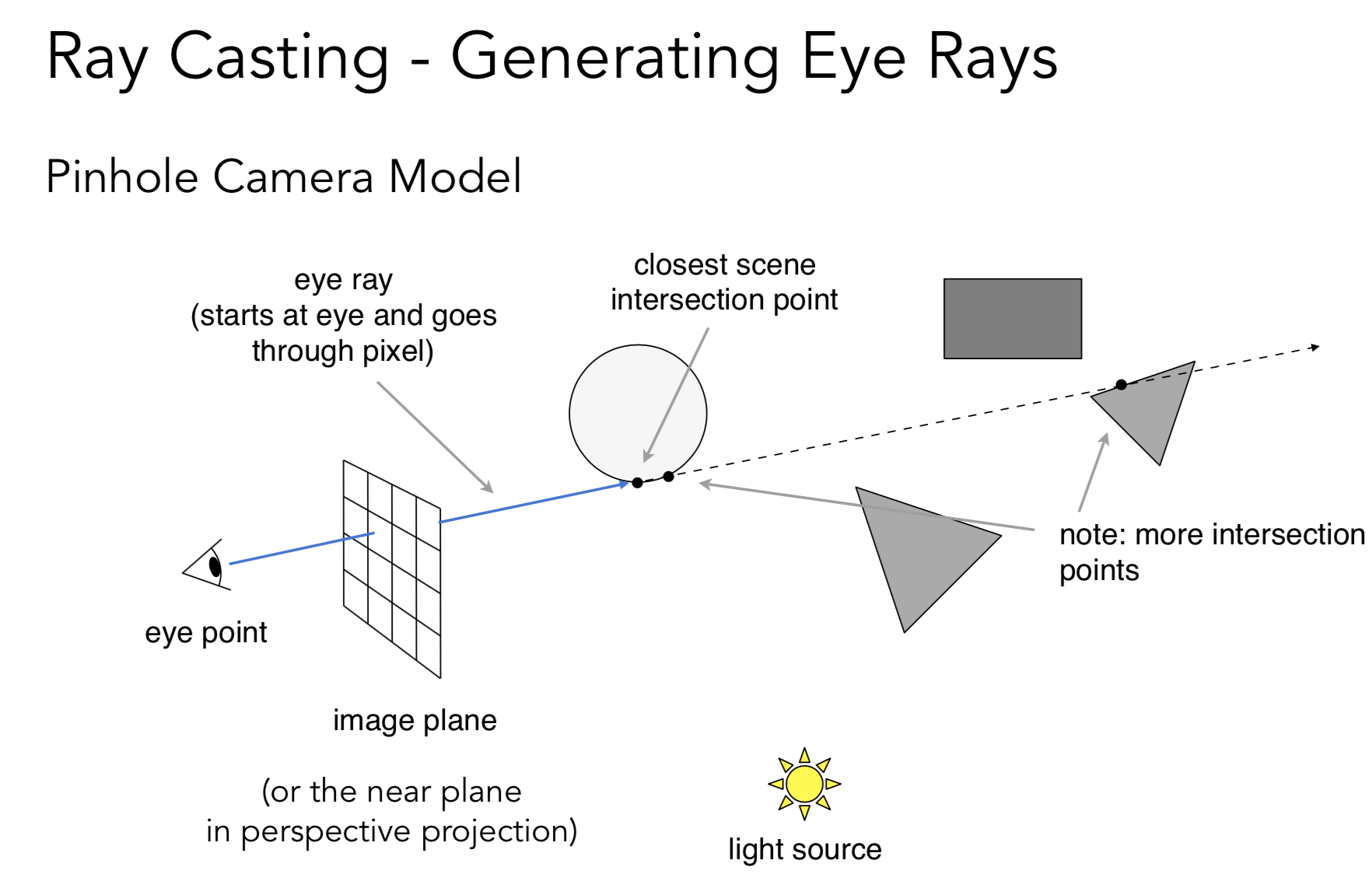
沿着一根光线, 记录最近的交点
光线追踪因为 ray 是从眼睛( 摄像机 ) 发出, 因此天然的解决了遮挡(深度测试)的问题,
早期人类认为人们能看见东西是因为从眼睛发射出射线， 尽管这并不符合现在的认知，但是根据光路的可逆性，是可以这样理解的。
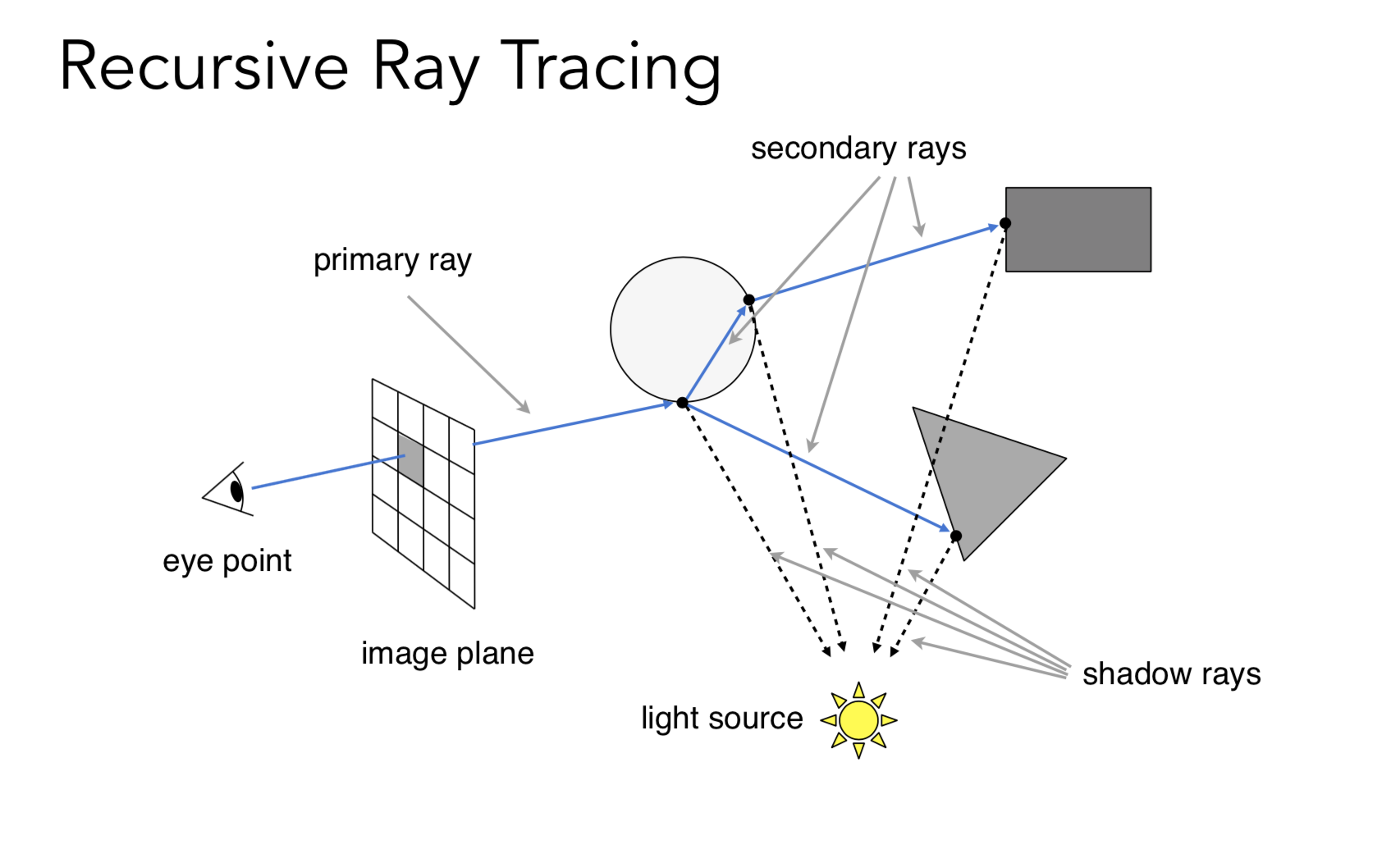
Whitted Style: 多次递归反射, 就是在模拟光线在不断弹射的过程.
eye ray 永远考虑和场景中的物体最近的点 (完美解决了深度问题)
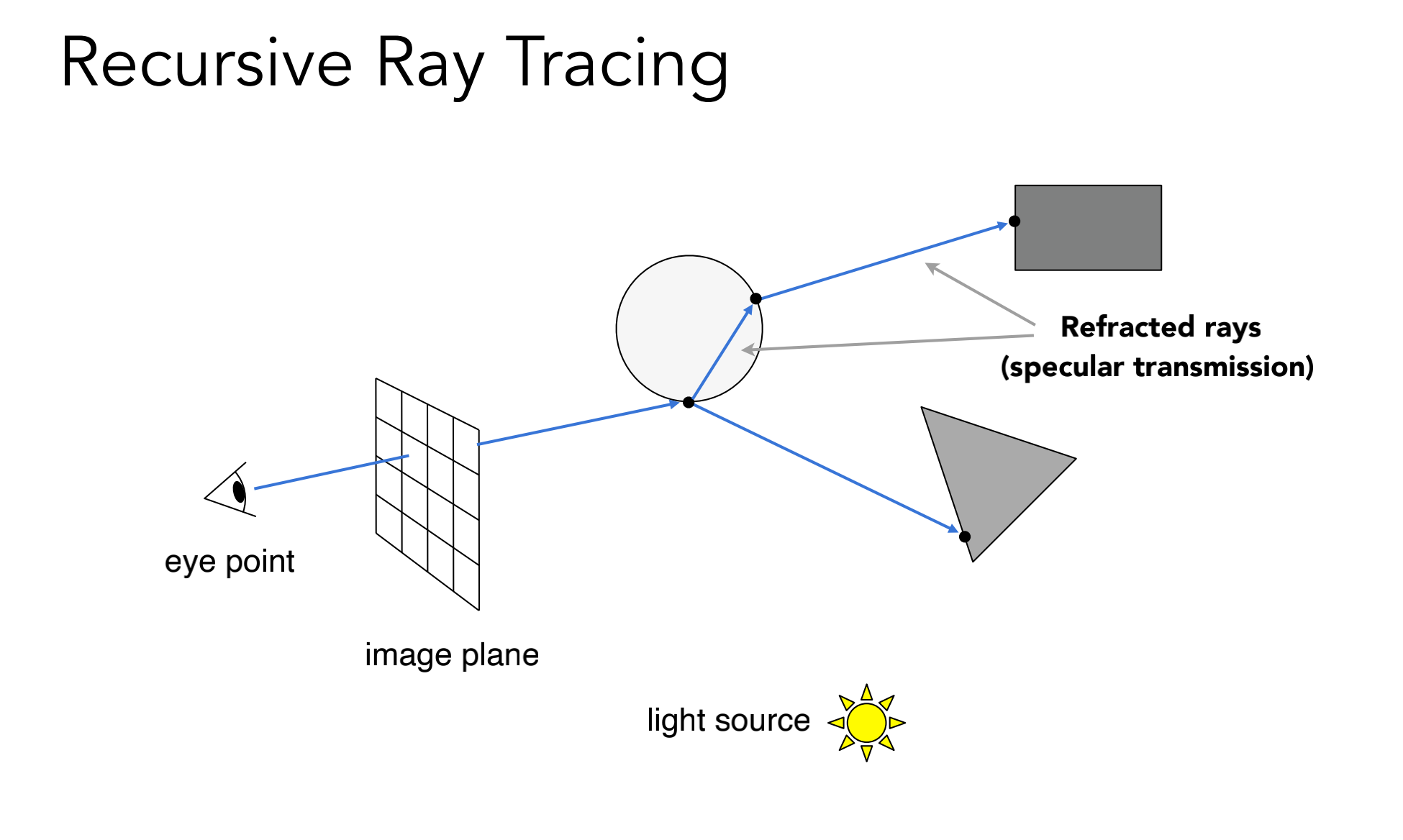
下面是一个玻璃球, 既有折射, 又有反射. 同时还要计算和光源的情况.
其实从这个图可以看到 光路有很多条, 最终我们要计算的是他们的和 (每条光路存在能量损失, 不然加起来光线亮度就很亮了)
whitted style 对于玻璃等电解质是递归的
在任意一个点可以继续传播射线，只要计算好反射和折射方向。
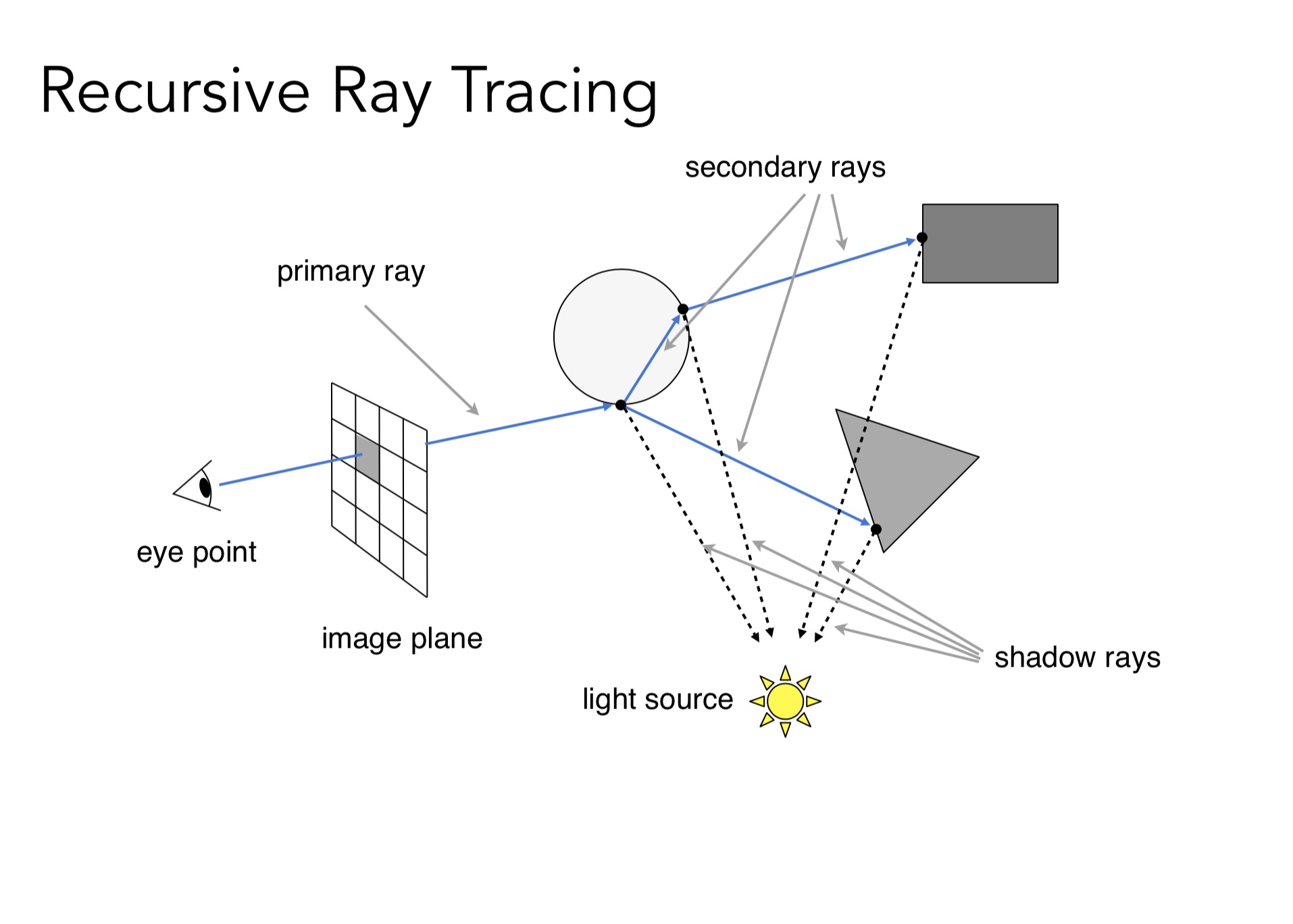在射线和物体的每一个交点，都和光源连线, 计算着色， 最终把这些着色加起来， 反映在像素点上。(被挡住的除外)
Read More https://zhuanlan.zhihu.com/p/144403005
PS: 这里提到了 RayTracingInOneWeekend, 这本书中提到的 whitted style ray tracing 和经典的有些不同。zhihu文章也说到 经典的whited-style光线追踪遇到漫反射表面会直接利用blinn-phong模型计算颜色值返回，而不再递归下去。
O + td
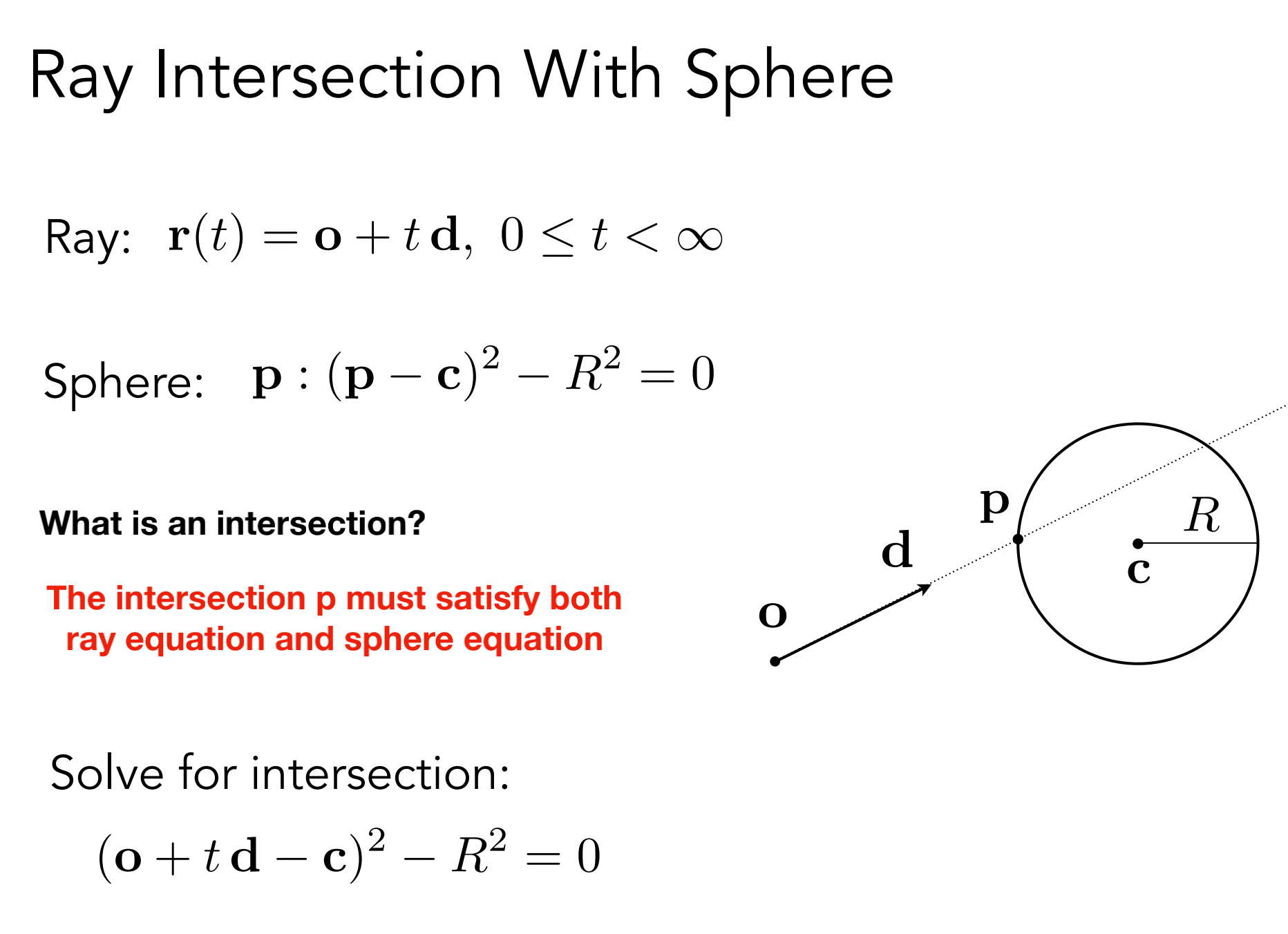
O 是光源位置
d 是光线方向
最后解除的 t 一定是正数
对于任何一种隐式表面 现在有很多工具可以利用数值法求解 甚至无需解方程
刚才 f(xx) = 0 是一个隐式表面的几何表达形式.
显式表面其实是求光线和三角形面的交点.
PS 通过光线和三角形求交点，可以判断是点否在物体内部。
如果一个点在封闭物体内部, 不论物体形状如何, 从这个点出发任意一条射线, 与物体的交点一定是奇数. 偶数的话一定是在物体外。
根据这个性质，可以用来判断是否在一个点是否在物体内部
该性质2D 3D 都满足
Read More 奇偶规则和非零缠绕规则 https://blog.csdn.net/g0ose/article/details/54933038
假设屏幕分辨率4K 我们要做的就是每一个像素都发出一条射线和模型的每一个三角形面求交点。
每一个三角形都计算一遍会很慢。 后面会介绍一些加速方法
先判断和平面相交, 再判断交点是否在三角形中.
如何判断和平面是否相交呢? 光线的定义已经有了 o + td 那么如何定义平面呢?
通过法线 和某一个点 其实就定义了平面
通过点法式（通过法线和一个点定义的平面）（图中左边的式子） 很容易判断一个点是不是在平面上
PS : 两个向量点乘是0 表示相互垂直 (p' 是平面上任意一个点)
More http://kjwy.5any.com/gdsx22/content/ch01/gdsx070501.htm
和前面和球球交点问题一样, 交点即在平面上 又在光线上. 因此两个公式都满足.
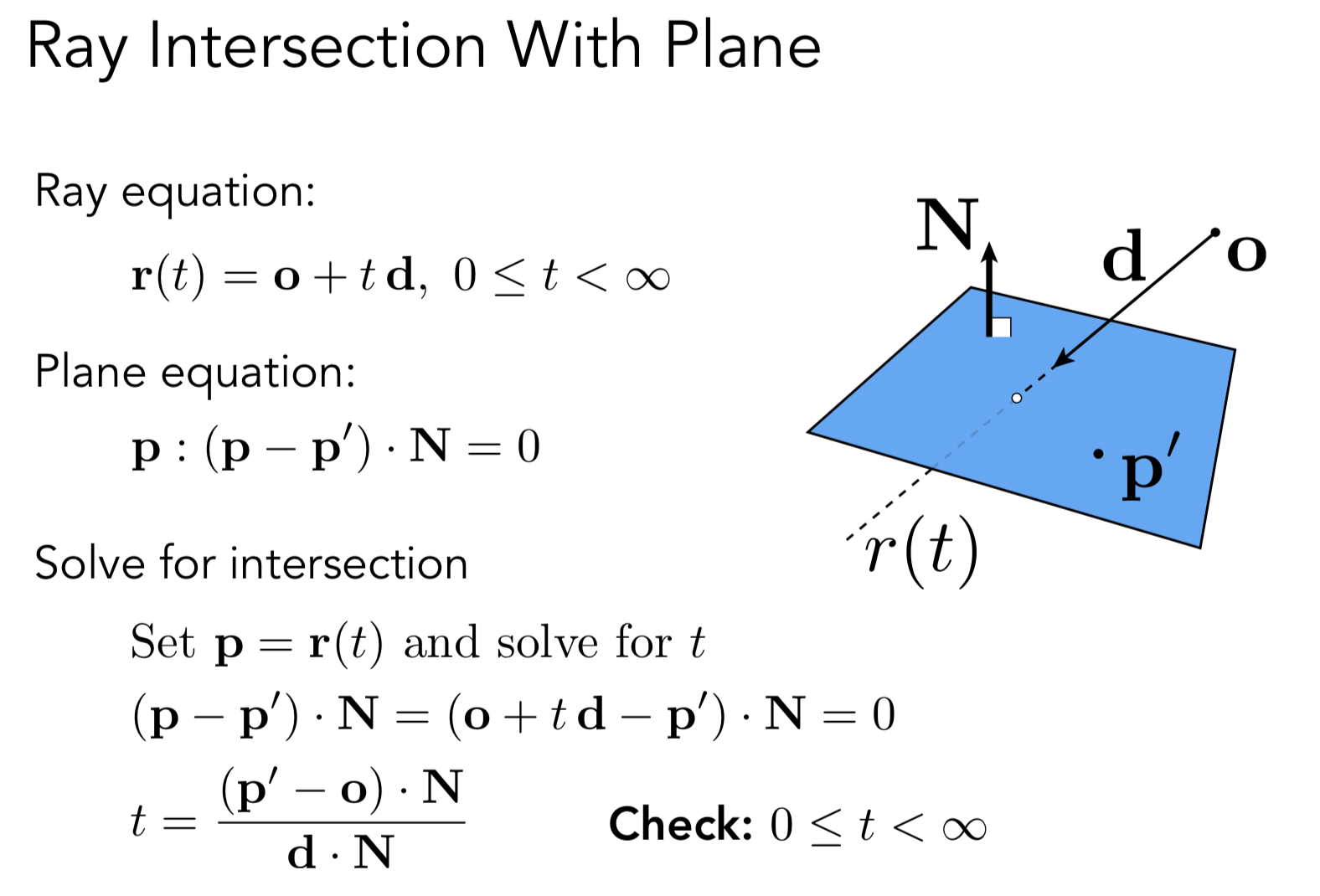
之后判断点是否在三角形内（之前在点乘的时候介绍过方法）
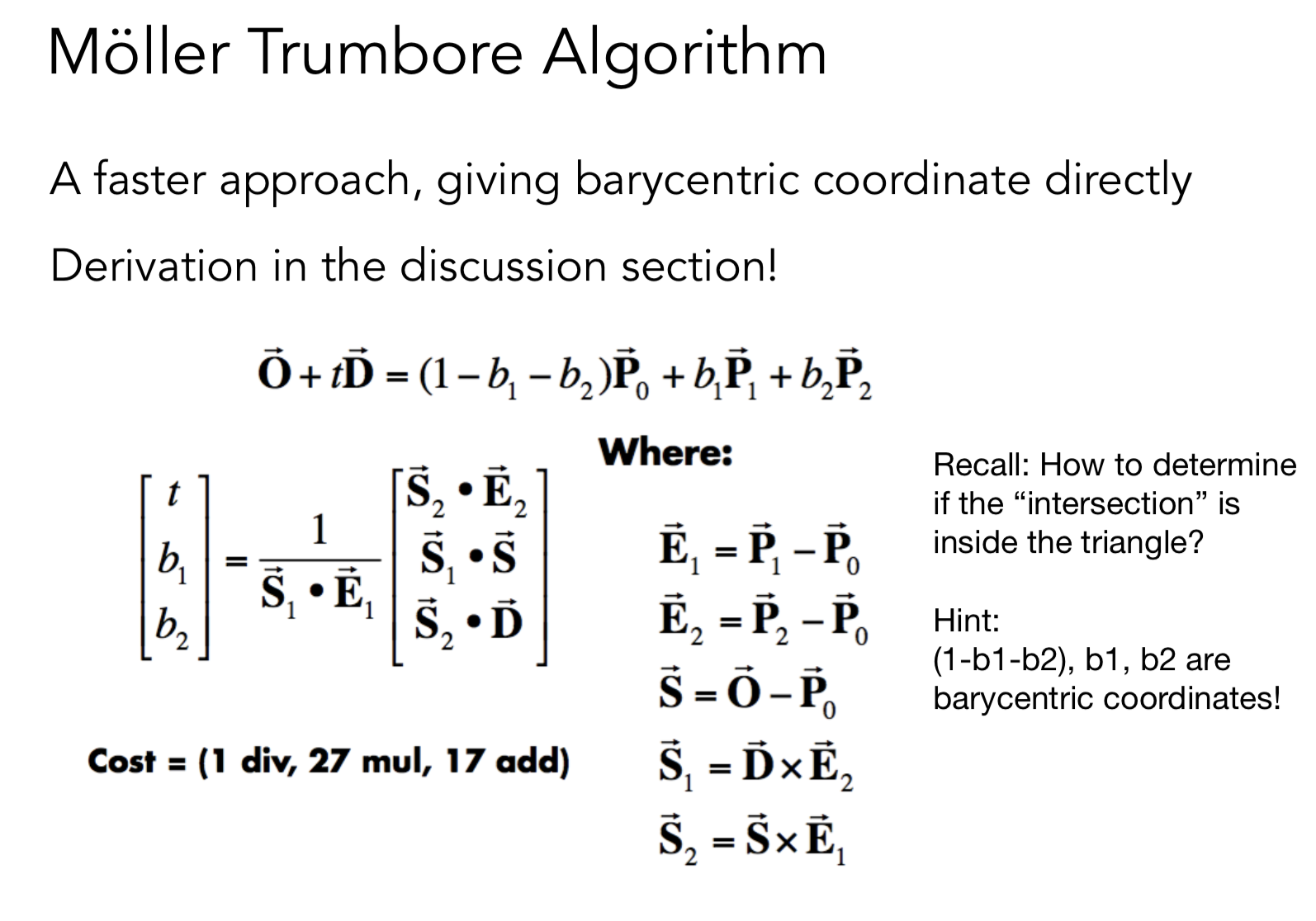
Möller Trumbore MT 算法
如果有解(满足 t > 0 && b1 >0 && b2 >0 && 1 - b0 - b2 > 0 )，得到的结果是一个重心坐标。
注意公式中的 1 - b1 -b2 , 点既然在三角形内, 那么这个点可以使用重心坐标去表示. (重心坐标的一个性质就是 b1+ b2 + b3 = 1)
剩下的部分就是解方程组了
图中底下一大串是用来判断方程组是否有解 More 克莱姆法则 https://zh.wikipedia.org/wiki/%E5%85%8B%E8%90%8A%E5%A7%86%E6%B3%95%E5%89%87
刚才说到和每一个三角形求交点很慢 如何加速呢
用来减少没有必要的计算
我们的摄像机, 也就是你所看到的屏幕. 每个像素都要发出一条光线, 和场景中所有的三角形求交点, 然后光线还要不断反射. 这样太慢了 怎么帮
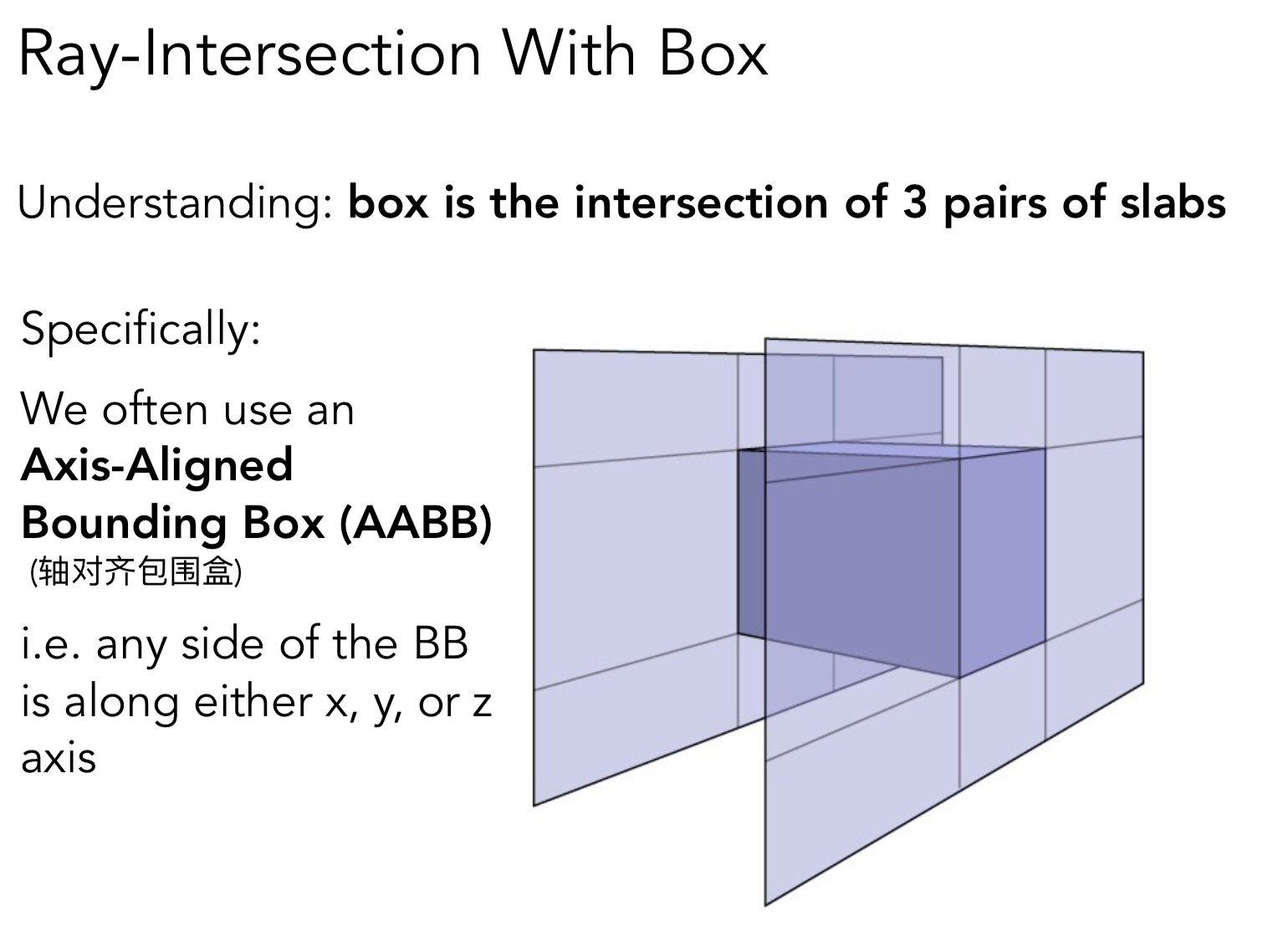
AABB能加速是基于这么一条结论: 如果光线都不和包围盒相交, 那么光线更不和可能和包围盒中的物体相交. 所以可以利用包围盒做加速
这个立方体上下左右前后 3对对面, 形成一个包围盒.
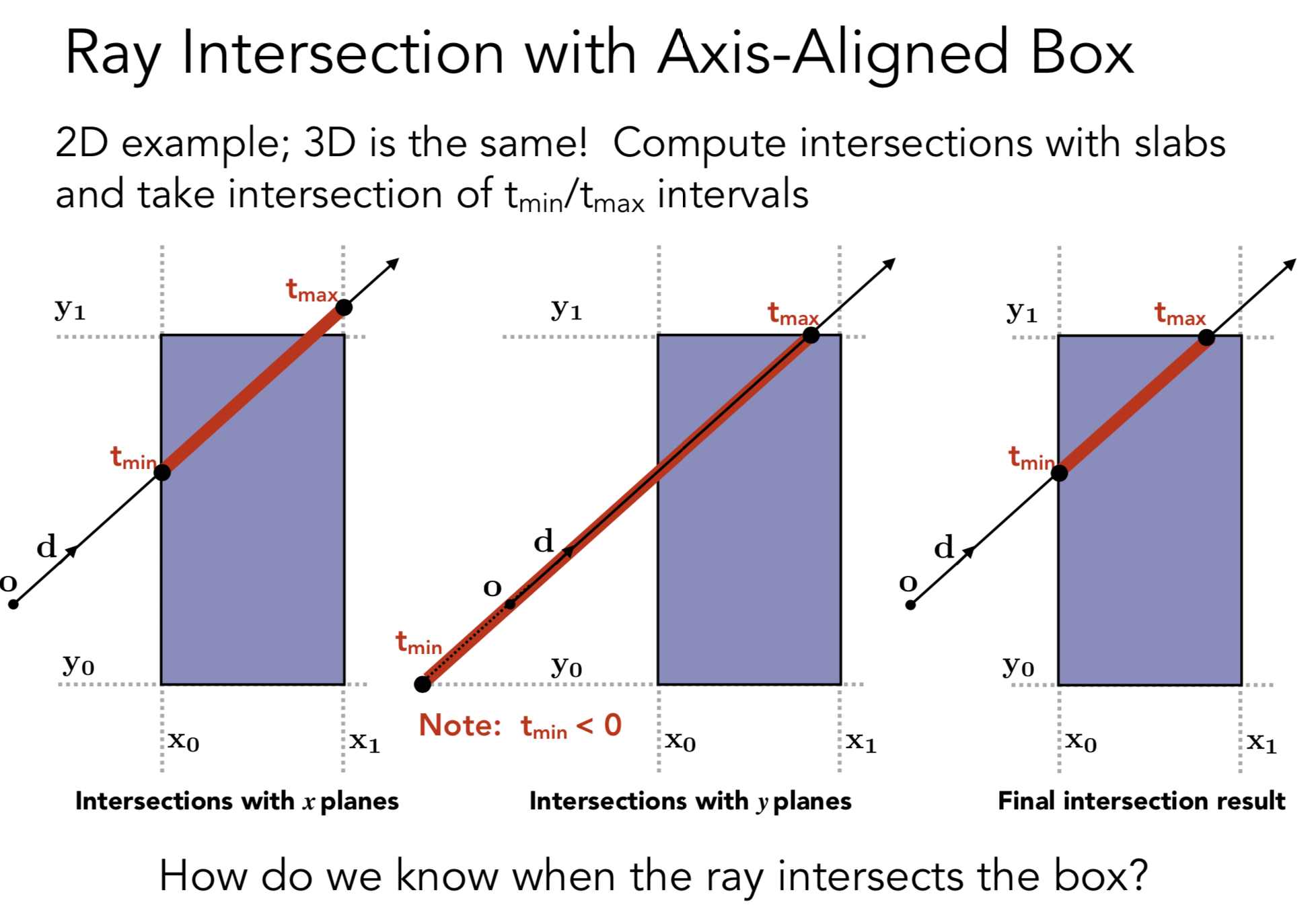
先看2D 情况下的包围盒
光线射入, 记录下碰到对面1 的时间 和 离开对面2 的时间.
Tenter Texit 是射线和盒子交汇的时机， 没有交点通过延长线求交点。
任何一组对面， 都可以求出光线进入和出去的时间 (即便是负数也OK， 有负数解是其中一种情况光源在这组对面内)
最终的包围盒中的射线, 是这三者求交集
如果 Texit < 0 表示没有交点 这里隐含的说明了 Tenter < 0 (因为 Tenter < Texit )
如果 Tenter < Texit 表示光线在盒子中停留过一段时间，可能有交点
https://zhuanlan.zhihu.com/p/144403005
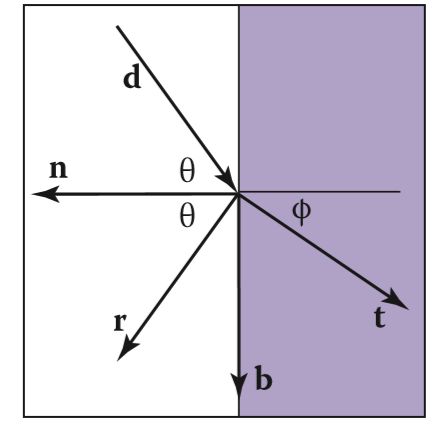
根据入射方向和法线， 两个不同介质的折射率，求出折射方向。
可以简单的理解左半部分是空气 右半部分是某个折射率高于空气的物体。最终需要求出的就是折射方向
描述了光线经过两个介质的界面时，反射和透射的光强比重。 Read More Read More
当光波从介质1传播到介质2时 入射光和法线的夹角θ1 折射光和法线夹角θ2 满足
n1*sinθ1=n2*sinθ2