Wordle is a web-based word game created and developed by Welsh software engineer Josh Wardle, and owned and published by The New York Times Company since 2022. Players have six attempts to guess a five-letter word, with feedback given for each guess in the form of colored tiles indicating when letters match or occupy the correct position. (description sourced from Wikipedia)
Wordle has gained much popularity since the start of 2022. According to an article by The Conversation. Wordle has nearly 3 million players across the world and versions of it are appearing in other languages.
With the growing popularity, the conversation of solving Wordle is a highly by individuals from various circles. A topic of much debate within the community is the choice of starting word.
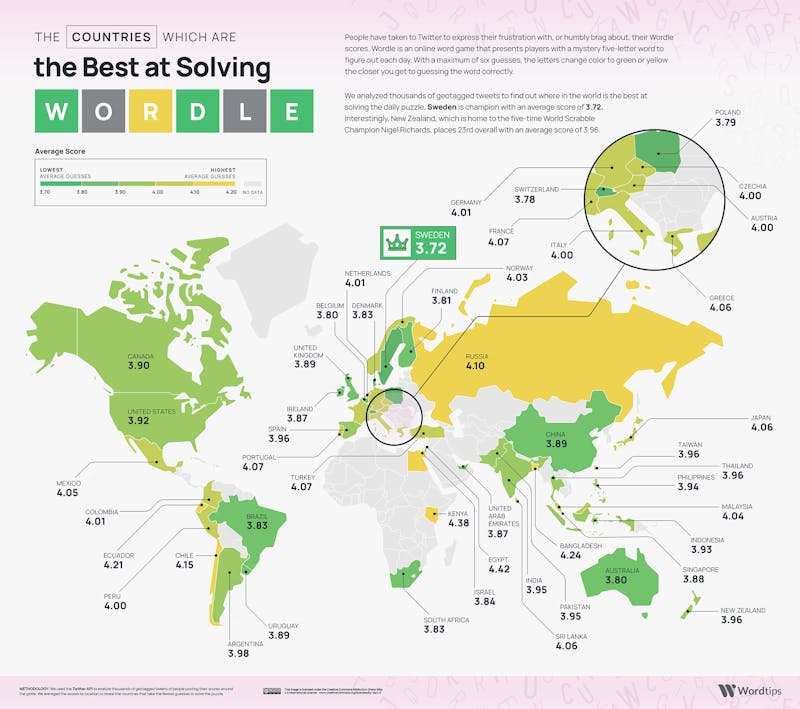
Below is a visualisation map depicting the average attempts it takes for a player to solve Wordle by country:
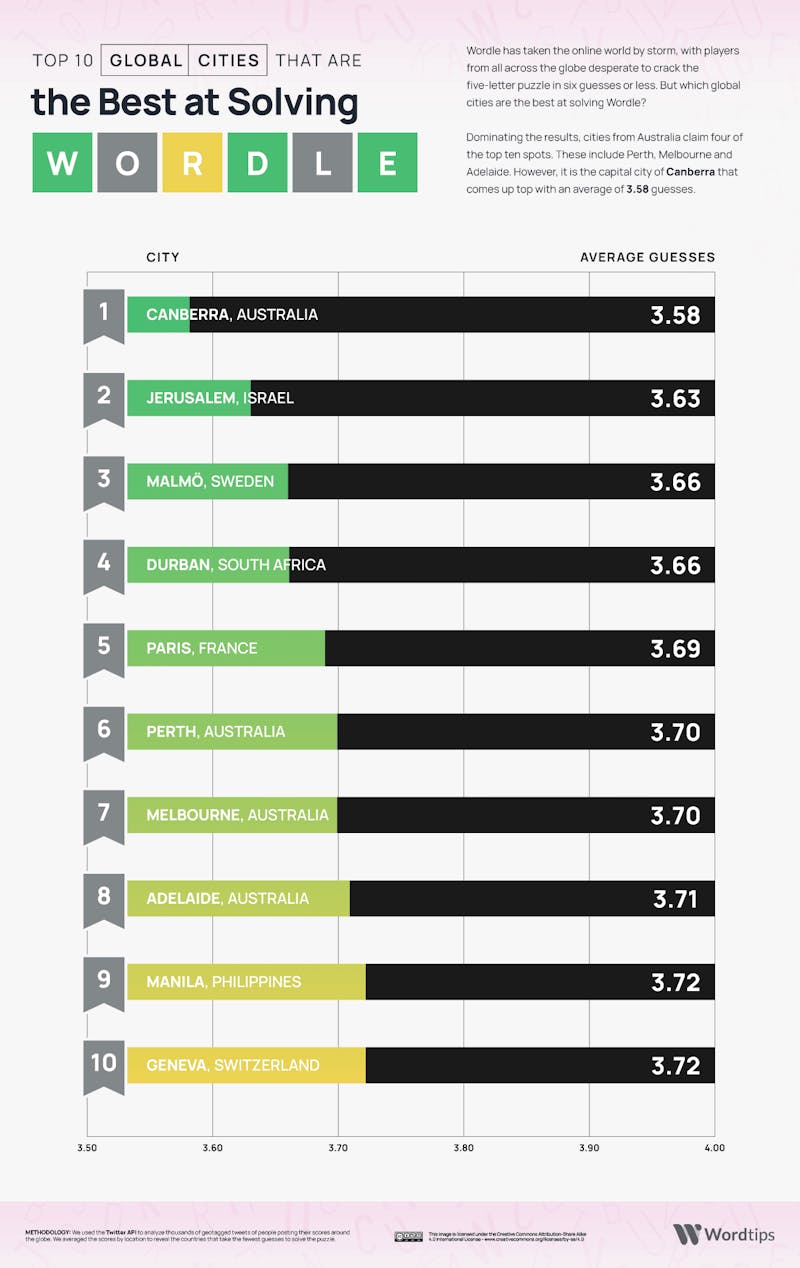
Below is a visualisation depicting the average attempts it takes for a player to solve Wordle on a city level:
Image Sources: Word Tips
For our final project we attempt to build an algorithm to solve Wordle.
For our first iteration, we attempted solve Wordle in the most naive possible way - Random Guessing. The approach is simple enough and easy to implement, but unsurprisingly performs poorly in practise. We performed simulations of all 2316 games (the size of the Wordle dictionary), and the solver was able to win very few games.
An improvement to build on our previous iteration involved solving the game more tactfully. This approach involved using the feedback (the letter colours) to reduce the search space for the next guess, thereby reducing the search space after every step and making guesses with slightly more finesse. While we reduced the search space with signficant effect, there was still an element of "randomness" with regards to choosing a word from the pool for the next guess.
Below we see a histogram depicting the performance of a simulation of this approach for all games:
We see that a simple change results in a solver capable of winning ~97.8% of the games! Can we do better than randomly selecting a word from a filtered pool?
The biggest hinderance with the previous iteration's solver comes from making guesses "randomly" from the pool of choices. In order to improve on this we need to quantify the value of each word. In order to do so, we leverage Information Theory . This is a well studied field that comes at the intersection of probability, statistics, computer science among other fields. The central theme of Information Theory is to capture "entropy" which can be thought of as a measure of uncertainty associated with a Random Variable. Our goal is to perform something similar where we aim to reduce the uncertainty within our pool of possible words, which are each equally likely, down to the one correct word to win the game.
We will be making using of a modified version of the Expectation Equation, as seen below to capture this uncertainty metric.
In essence, we hope to create a metric that helps us capture how much uncertainty would entering in a particular word reduce, on average, to help us reduce our search space. Higher the number better.
A seemingly, intimidating equation, but when broken down this is a very easy metric to compute and intuitivly understand.
The expected information obtainable from a guessing a particular word, or simply as we've dubbed as "xG" is the sums of the probability of encountering a particular response (a 5 lettered permutation of grey, yellow, and green tiles) times the the negative log of this probability.
So what does this metric tell us about starting words?
"Raise" is the best word to start the game with. This seems like fairly intuitive for good and bad choices given that raise has 3 vowels, and the letters "r" and "s" both which are fairly frequent. The worst word to start the game off on the other hand is with "fuzzy". Two occurances of the letter "z" - seems fairly obvious again.
Below is a sample of some of the good and bad choices to start the game off with.
How does it perform?
Below we see a histogram depicting the performance of a simulation after appending the above formulation for all games:
We see that this approach has improved things significantly. Not only are we able to win 99.58% of the games (nearly 2% improvement), but also a signficant drop in the average guesses needed to 3.62 guesses. This is better than the average human from the best performing country at Wordle, and second best (to Canberra) when compared to the city averages.
Throughout our project we extensively made use of Pandas Dataframes. They were especially useful with storing words (as individual letters), filtering out unlikely words, calculating probabilites, xGs, etc.
Validating a word choice: O(n)
Filtering by a letter (green): O(n)
Filtering by a letter (grey): O(m * n) m-> length of word; n -> size of dictionary; Can be approximated to O(n), since m = 5 is constant, i.e., O(1)
Filtering by a letter (yellow): O(m * n) m-> length of word; n -> size of dictionary; Can be approximated to O(n), since m = 5 is constant, i.e., O(1)
Calculating xG: O(n * n * n) + O(n) ~ O(n * n * n) or O(n^3); This can be brought down to O(n^2) through Dynamic Programming.
- Two Level xG - our approach calculates the xG metric for a single word to optimise for the best choice. Integrating a two level xG, where we also optimise our choice of first word to also consider the options for the second choice of word could potentially improve things
- Calculating xG with more finesse - every time we make a guess and our pool of words reduce, we recalculate the xG for each word all over again. This is time consuming and a very poor algorithmic choice given that the xG values for the updated dictionary can be potentially be recalculated without having to recalculate from scratch all over again.
- N-Wordle - Extend Wordle to play for words beyond the length of 5 letters.
- Quordle - A 4x variant of Wordle which poses additional challenges.
A lot of our ideas were inspired by the YouTuber 3Blue1Brown who covered the topic of Wordle and Information Theory in their channel .